Seventh circle theorem proof
You are here: Home > Maths intro > Circle theorems first page > Alternate segment proof
'The angle (α) between the tangent and the chord at the point of contact (D) is equal to the angle (β) in the alternate segment'[A printable version of this page may be downloaded here.] 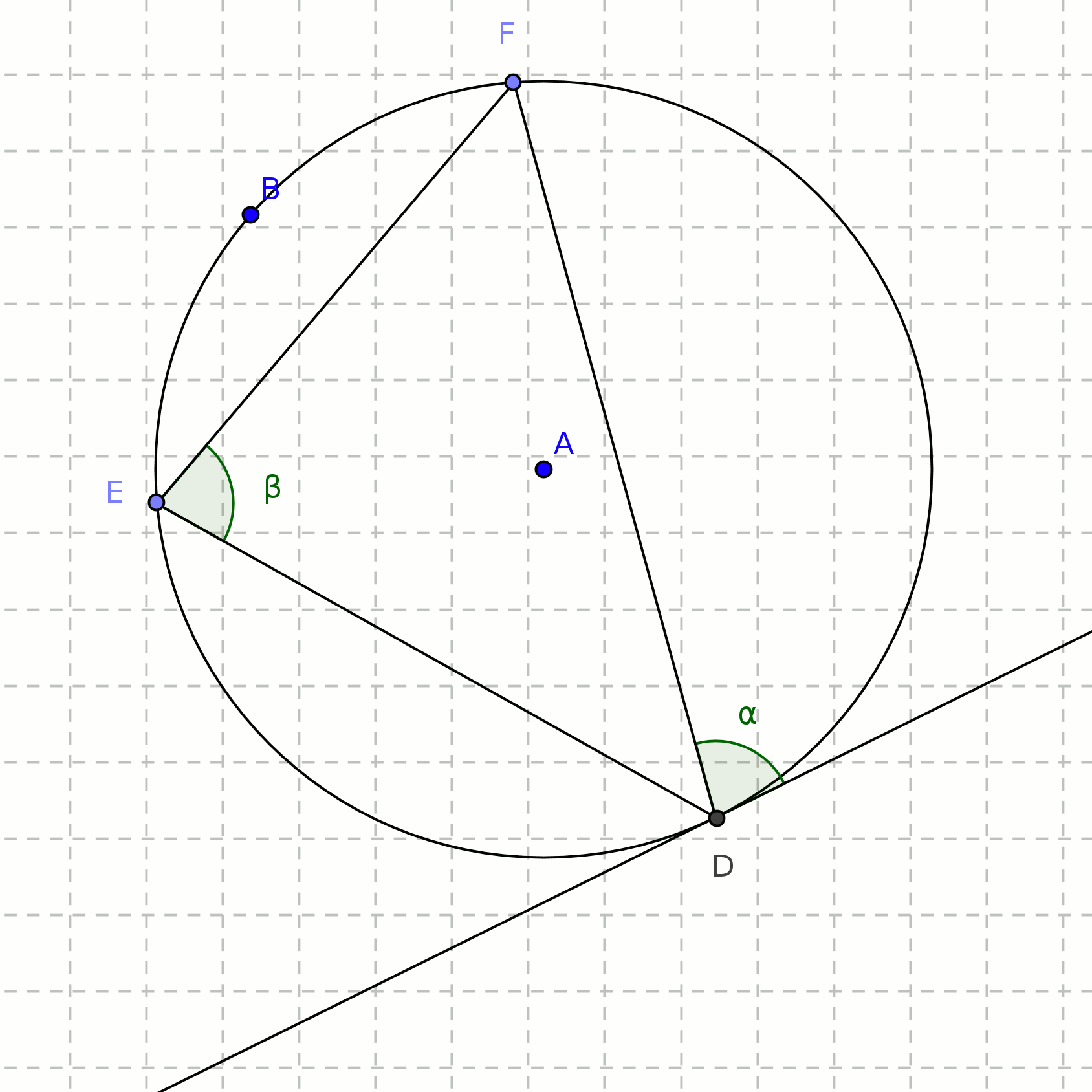
Fig 1 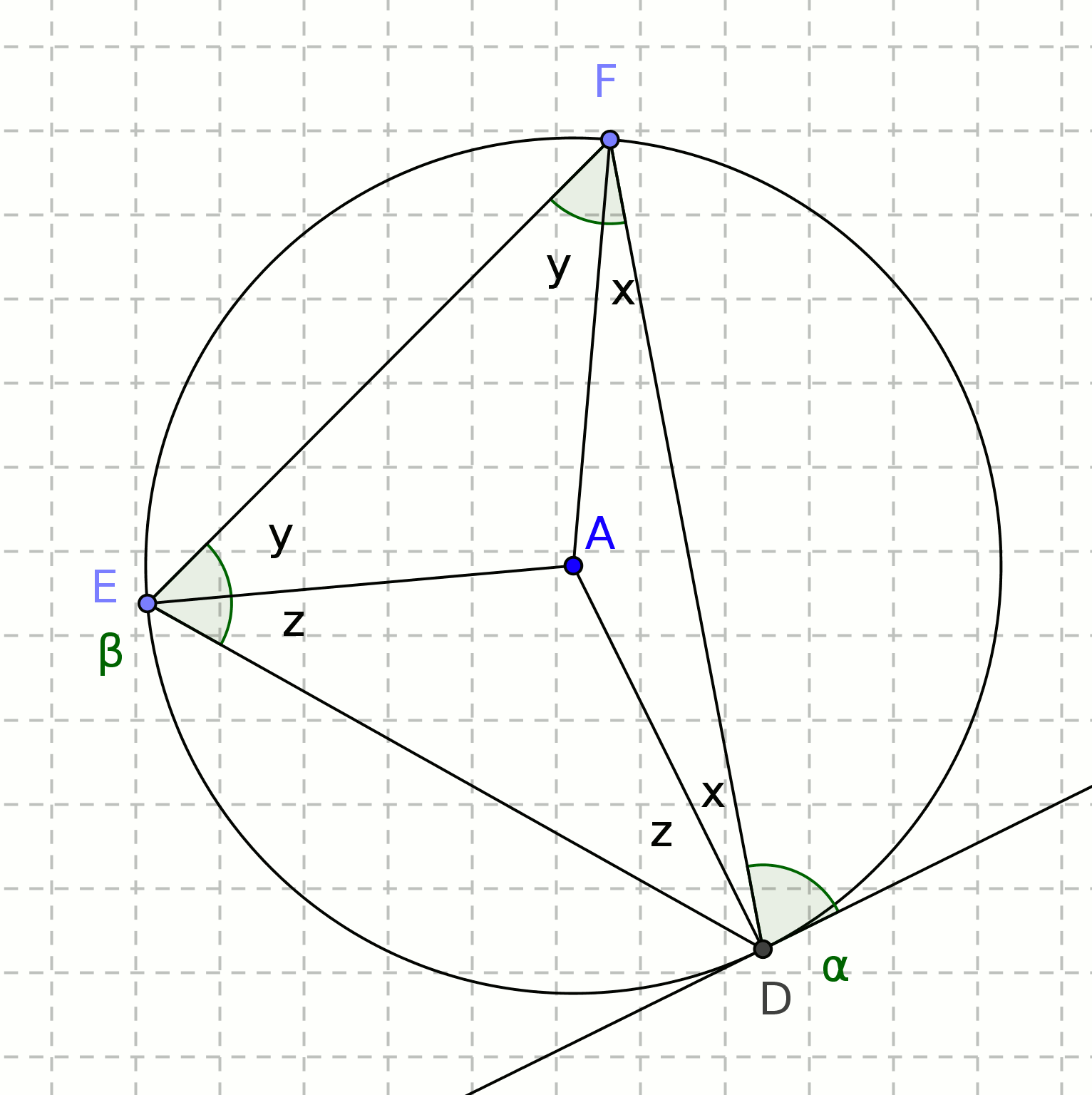
Fig 2
The chord DF divides the circle into two segments, and we're interested in the angle between this chord and the tangent at D, and the angle in the other (alternate) segment, E. |