Eight circle theorems page

The Theorems

Download them as a .pdf file which summarises the theorems - basically a hard-copy, 2 sides of A4, version of this page.

Here, I've set out the eight theorems, so you can check that you drew the right conclusions from the dynamic geometry pages! I've included diagrams which are just dull static geometry, partly as a back-up in case the dynamic pages didn't work on your computer. I've also recently popped in more links back to the dynamic geometry pages: for example, you can just click on the diagram. I notice that Google seems to land you here if you were Searching for 'Circle Theorems', so you may not yet have seen the full dynamic delights lurking a mere click away!!!

Technical note

With a bit of luck, the next paragraph should be irrelevant now - I've updated the Dynamic Geometry pages to use Geogebra 5 & Geogebra Tube.

If you get "Error. Click for details" where the dynamic geometry ought to be, it may just be worth reloading the page. If that doesn't work, it probably means Geogebra have changed the location of a crucial file, & I haven't updated the pages!!

If you have problems with the pages, or want to get in touch, let me know.

Tim Devereux 2/2/15

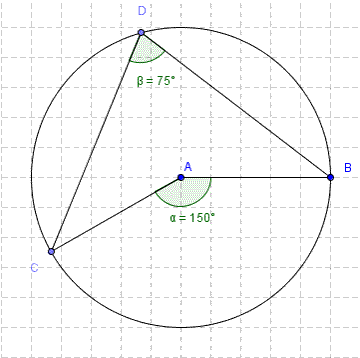
• First circle theorem - angles at the centre and at the circumference.
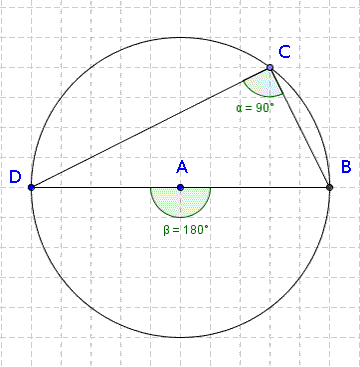
• Second circle theorem - angle in a semicircle.
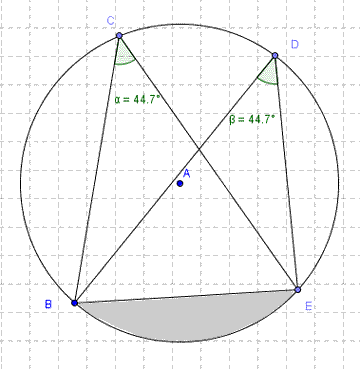
• Third circle theorem - angles in the same segment.
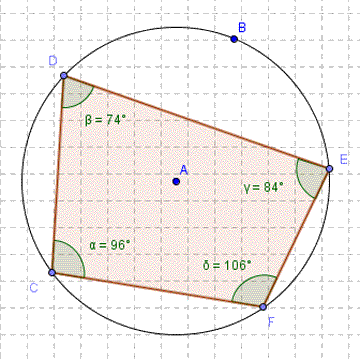
• Fourth circle theorem - angles in a cyclic quadlateral.
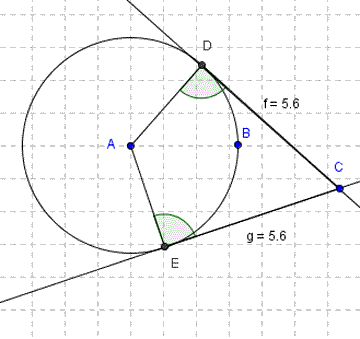
• Fifth circle theorem - length of tangents.
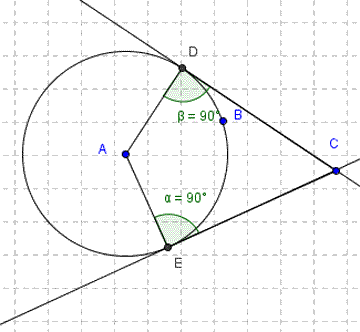
• Sixth circle theorem - angle between circle tangent and radius.
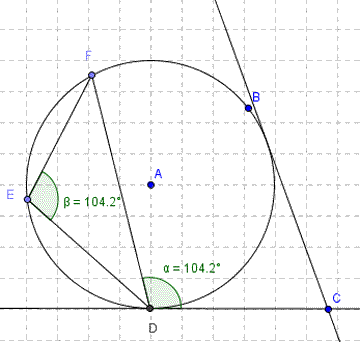
• Seventh circle theorem - alternate segment theorem.
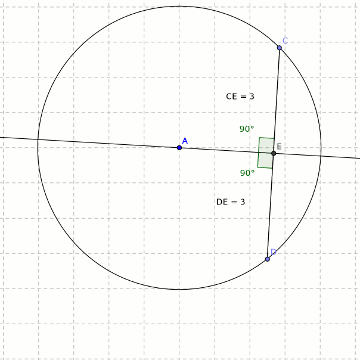
• Eighth circle theorem - perpendicular from the centre bisects the chord

Circle Theorem 1

link to dynamic page

The angle at the centre is twice the angle at the circumference.

(Note that both angles are facing the same piece of arc, CB)

Circle Theorem 2

link to dynamic page

The angle in a semi-cicle is 90°.

(This is a special case of theorem 1, with a centre angle of 180°.)

Circle Theorem 3

link to dynamic page

Angles in the same segment are equal.

(The two angles are both in the major segment; I've coloured the minor segment grey)

Circle Theorem 4

link to dynamic page

Opposite angles in a cyclic quadrilateral add up to 180°.

Circle Theorem 5

link to dynamic page

The lengths of the two tangents from a point to a circle are equal.

CD = CE

Circle Theorem 6

link to dynamic page

The angle between a tangent and a radius in a circle is 90°.

link to dynamic page

Alternate segment theorem:
The angle (α) between the tangent and the chord at the point of contact (D) is equal to the angle (β) in the alternate segment*.

*Thank you, BBC Bitesize, for providing the precise wording for this theorem!
Here's a link to the their circles revision pages.

link to dynamic page

Perpendicular from the centre bisects the chord:

DE = CE