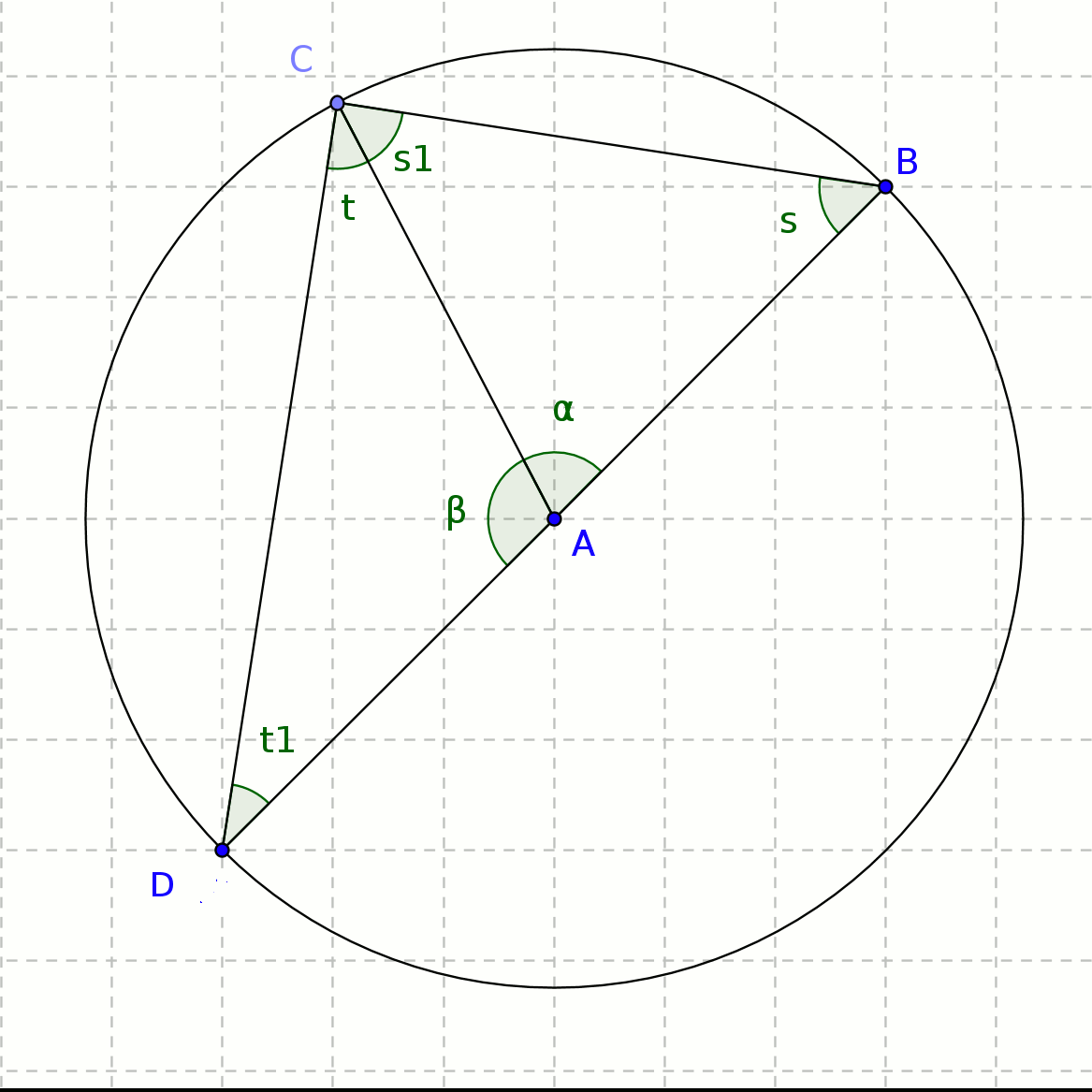
Fig 1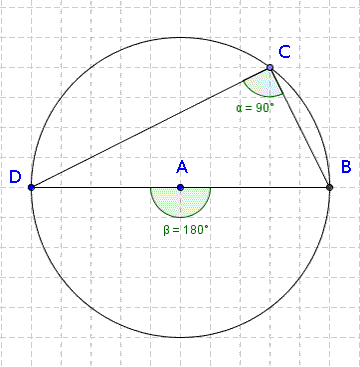

Fig 2

In Fig 1, BAD is a diameter of the circle, C is a point on the circumference, forming the triangle BCD. The angle BCD is the 'angle in a semicircle'.
Radius AC has been drawn, to form two isosceles triangles BAC and CAD. They are isosceles as AB, AC and AD are all radiuses.

So in BAC, s=s1 & in CAD, t=t1

Hence α + 2s = 180 (Angles in triangle BAC)

and β + 2t = 180 (Angles in triangle CAD)

Adding these two equations gives:
α + 2s + β + 2t = 360

But α + β = 180 (angles on a straight line)

so 180 + 2s + 2t = 360

ie 2s + 2t = 180

so s + t = 90

hence angle BAC = 90

ie, 'Angle in a semicircle is a right angle'

QED

---

[Of course, looking at Fig 2, you could just use theorem 1: angle BAD is 180 degrees and is the 'angle at the centre', and BCD is the 'angle at the circumference', so must be half of 180 degrees, ie 90 degrees....]